Convolution Layer
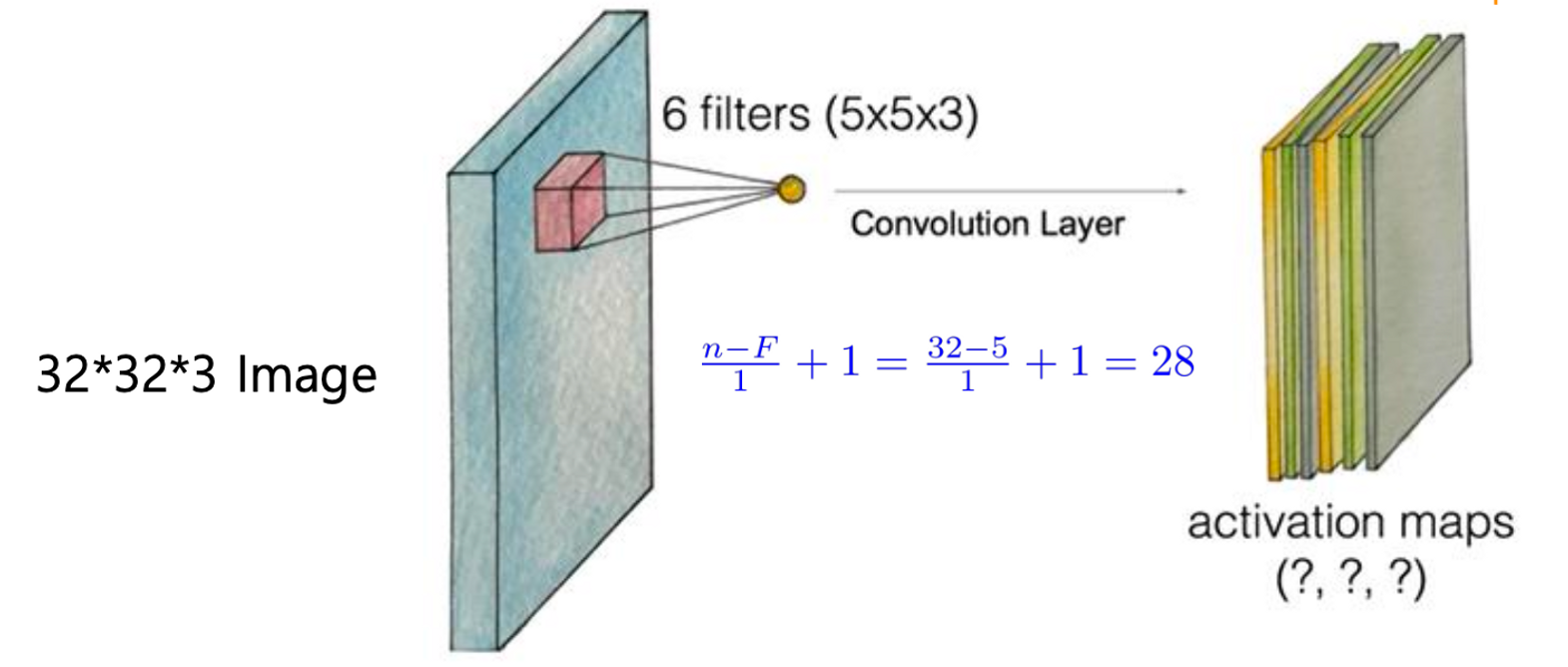
위 그림을 살펴보자. 맨 왼쪽에 있는 이미지의 크기는 32*32이며 3개의 채널을 가지고 있다.
그리고 이 이미지 중간에 붉은 색으로 표현된 부분은 필터이다. 필터의 크기는 5*5이며, 이미지 채널의 수와 같은 3개의 층을 가지고 있다. 각 채널 별로 다른 층의 필터를 통과시키려는 의도라고 볼 수 있다.
$$\frac{(N-F)}{Stride}+1=\frac{32-5}{1}+1=28$$
앞서 배운 이동 횟수를 구하는 공식에 따라 위와 같이 결과값 레이어의 크기는 28*28임을 알 수 있다.
결과값 레이어의 층은 필터의 수에 영향을 받는다. 위 그림의 경우에는 6 filters를 사용한다고 했으니 결과값 레이어는 28*28*6 구조를 가질 것이다.
필터를 여러 개 사용하는 이유는 가중치를 바꿔가며 여러가지 상황에서의 특징을 검출하기 위함이다.

위 사진과 같이 여러 개의 Convolution Layer를 거칠 수도 있다. Padding 관련 설정에 따라 Convolution Layer를 거치는 과정에서 이미지의 크기가 줄어들기도 하며, 결국 원본 이미지에 있던 정보가 점점 줄어들어 특징만 남게 된다.
종종 필터의 크기를 1*1*3으로 설정하는 경우가 있는데, 이에 대한 장점에는 다음과 같이 있다.
- 추정해야 할 파라미터의 양이 감소하여 계산량이 줄어든다.
- 국소적인 픽셀에 ReLU 함수를 적용하여 비선형성을 강조하는 모형을 만들 수 있다.
ReLU 함수는 '6주차' 내용에서 살펴볼 수 있듯이 음수 부분을 0으로 만들어 선형성을 방지하는 함수이다. 딥러닝 모형에서 비선형성을 강조하는 것은 복잡한 패턴과 상호작용을 학습하기 위해서 필요한 작업이다.
만약 선형 모델로 설계된다면 입력과 출력 간의 단순한 선형 관계만을 학습할 수 있기 때문에 딥러닝 모형에 적합하지 않다.
Convolution Layer 통과 횟수에 따른 경향

위 그림은 이미지가 Convolution Layer를 통과함에 따른 변화를 나타내고 있다.
여러 개의 Convolution Layer를 통과할 수록 점점 대략적인 큰 특징들을 요약하게 된다. 반면에 적은 수의 레이어를 통과하면 국소적인 부분의 특징만 요약할 수 있다.
Pooling Layer

앞서 Pooling Layer에 대해 설명할 때 입력받은 내용 중, 뚜렷한 부분만을 남기는 역할을 한다고 했다.
이러한 Pooling Layer에서 많이 사용되는 방식으로 입력 레이어 중, 가장 큰 값만 Sampling하는 Max Pooling 방식이 있다.
$$\frac{(N-F)}{Stride}+1=\frac{4-2}{2}+1=2$$
위 그림은 2*2 커널(필터같은 개념)을 2*2 Stride(한 번에 2칸 씩 이동)를 사용해 얻은 결과물이다. 위 식에 따라 결과 데이터는 2*2의 크기를 가지게 된다.
딥러닝과의 관계

위 그림과 같이 입력 데이터와 출력 데이터 사이에는 여러 Convolution Layer와 Pooling Layer를 거친다. 이를 통해 특징이 되는 부분만 남게 된다.
이렇게 특징만 남은 이미지를 딥러닝에서 학습할 데이터로 사용한다.
수치적으로 CNN 이해하기

CNN 과정을 수치적으로 이해해보도록 하자.
원본 이미지의 파라미터는 (1, 3, 3, 1)로 주어졌다. 첫 번째 파라미터는 입력 이미지가 1개임을 나타내며 두 번째와 세 번째 파라미터는 이미지의 크기가 3*3임을 나타낸다. 마지막으로 네 번째 파라미터는 색상(채널)이 1개임을 나타낸다.
다음으로 필터의 파라미터는 (2, 2, 1, 1)로 주어졌다. 첫 번째와 두 번째 파라미터는 필터의 크기가 2*2임을 나타내며 세 번째 파라미터는 색상(채널)이 1개임을 나타낸다. 마지막으로 네 번째 파라미터는 필터의 수가 1개임을 나타낸다.
Stride는 한 번에 필터가 이동하는 크기를 나타낸다.
Padding이 Valid라는 의미는 Padding이 없으므로 이미지의 크기가 작아지는 것을 허용한다는 의미이다.
$$\frac{(N-F)}{Stride}+1=\frac{(3-2)}{1}+1=2$$
위 그림 속 과정의 결과 이미지의 크기는 위와 같은 계산을 거쳐 2*2임을 알 수 있다.
image(이미지의 수, 행의 수, 열의 수, 채널 수)
filter(행의 수, 열의 수, 채널 수, 필터의 수)방금 언급한 파라미터들에 대한 내용을 정리하자면 위와 같다.
Mnist Data 적용
#Mnist_convLayer.ipynb
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from tensorflow.keras import datasets
from tensorflow.keras.utils import to_categorical
mnist = datasets.mnist
(train_x, train_y), (test_x, test_y) = mnist.load_data()
img=train_x[0]
plt.imshow(img, cmap='gray')
plt.show()
img=img.reshape(-1,28,28,1)
W1=tf.random.normal([3,3,1,5], stddev=0.01)
conv2d=tf.nn.conv2d(img, W1, strides=[1,2,2,1], padding='SAME')
conv2d_img=conv2d.numpy()
conv2d_img=np.swapaxes(conv2d_img,0,3)
for i, one_img in enumerate(conv2d_img):
plt.subplot(1,5,i+1), plt.imshow(one_img.reshape(14,14), cmap='gray'), plt.show()위 코드 중에서 W1=tf.random.normal([3,3,1,5], stddev=0.01) 부분을 살펴보면 Convolution Layer를 여러 개 만들기 위해 필터(weight)의 수를 5개로 설정한 것을 볼 수 있다.

그 결과 왼쪽과 같은 원본 이미지로부터 오른쪽과 같이 5개의 결과 이미지가 도출되는 것을 볼 수 있다. 5개의 결과 이미지가 각기 다른 모습을 가지는 이유는 필터마다 초기값이 난수로 지정되었기 때문이다.
이 과정에서 padding = ‘SAME’ 설정을 했음에도 이미지의 크기가 줄어든 것은 stride의 크기가 2이므로, 결과 이미지의 크기는 절반씩 둘어들어 14*14가 된다.
pool=tf.nn.max_pool(conv2d, ksize=[1,2,2,1], strides=[1,2,2,1], padding='SAME')
pool_img=pool.numpy()
pool_img=np.swapaxes(pool_img,0,3)
for i, one_img in enumerate(pool_img):
plt.subplot(1,5,i+1), plt.imshow(one_img.reshape(7,7), cmap='gray'), plt.show()이후 Pooling Layer를 만드는 과정이다.

위 그림은 Pooling Layer를 거친 결과 이미지이다. 핵심적인 부분만 추려진 것을 볼 수 있다.
Stride의 크기를 2로 주었기 때문에 결과 이미지의 크기는 7*7로 줄어든 것을 볼 수 있다.

위 그림은 지금까지 작업한 내용을 한 눈에 살펴본 것으로, 최종 결과를 Fully Connected Layer라고 부른다.
하나의 이미지로도 Convolution Layer, Pooling Layer를 거쳐 다양한 관점에서의 특징을 축약된 이미지들이 생성된다. 축약된 이미지를 통한 학습이 원본 이미지를 통한 학습보다 더 좋은 인식률을 가질 수 있다는 것이 CNN의 핵심이다
레이어 별 파라미터 수 계산
#image(이미지의 수, 행의 수, 열의 수, 채널 수)
#filter(행의 수, 열의 수, 채널 수, 필터의 수)
# Mnist_CNN_TF2.ipynb
import tensorflow as tf
from tensorflow.keras import layers, models from tensorflow.keras import datasets
from tensorflow.keras.utils import to_categorical
(train_images, train_labels), (test_images, test_labels) = datasets.mnist.load_data()
train_images = train_images.reshape((60000, 28, 28, 1))
test_images = test_images.reshape((10000, 28, 28, 1))
# 픽셀 값을 0~1 사이로 정규화합니다.
train_images, test_images = train_images / 255.0, test_images / 255.0
train_y_onehot = to_categorical(train_labels)
test_y_onehot = to_categorical(test_labels)
model = models.Sequential()
model.add(layers.Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1)))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Flatten())
model.add(layers.Dense(10, activation='softmax'))
model.summary()
위 코드에서는 이미지의 크기를 알아볼 수 있어야 하며, 이를 통해 결과 이미지에서 나온 파라미터의 수를 계산할 수 있어야 한다.
#Convolution Layer에서 파라미터 수 구하기
#가중치 = (필터 크기) * (필터 채널 수) * (필터 수)
#편향치 = (필터 수)
#파라미터 수 = (가중치) + (편향치)
#conv2d
가중치 = (3 * 3) * (1) * (32)
편향치 = (32)
파라미터 수 = 320
#conv2d_1
가중치 = (3 * 3) * (32) * (64)
편향치 = (64)
파라미터 수 = 18496Convolution Layer에서 각 레이어의 파라미터 수를 구하면 위와 같다.
#Dense Layer에서 파라미터 수 구하기
#가중치 = (이전 Layer의 뉴런 수) * (이후 Layer의 뉴런 수)
#편향치 = (이후 Layer의 뉴런 수)
#파라미터 수 = (가중치) + (편향치)
가중치 = (1600) * (10)
편향치 = (10)
파라미터 수 = 16010Dense Layer의 파라미터 수를 구하면 위와 같다.
지금까지 CNN을 실전 상황에서 사용하는 예를 살펴보았다. 입력된 데이터를 1차원 벡터로 Flatten하여 처리하는 히든 레이어 방식과 달리 CNN은 입력된 데이터가 2차원이더라도 필터를 사용하여 특징을 검출한다. 그리고 CNN을 사용한 모델의 정확도는 99%로 굉장히 높았는데 이를 통해 Convolution Layer, Max Pooling을 사용하여 이미지를 축약하는 것이 더 좋은 성능을 가져온다는 것을 알 수 있었다.