Cross Entropy Function들
$$ Cost(w) = \sum_{i = 1}^{n}{(-y_ilogH(X) - (1 - y_i)log(1-H(X)))}, \quad y_i = 0, 1$$
위 식은 이진 문제를 다루는 Binomial Logistic Regression의 Cross Entropy Funtion 식이다. 이러한 Cross Entropy Function을 다중 분류 문제에 사용할 때 사용하는 Muiltinomial Logistic Regression의 경우에 맞춰 작성하면 다음과 같다.
$$ Cost(w)=\sum_{i = 1}^{n}\sum_{j = 1}^{c}{(Y_{ij} * logH(X)_{ij})} $$
$$ Y = \left [ \begin{array}{cc} 1 & 0 \\ 0 & 1 \\ 0 & 1 \\ \end{array} \right], H(X) = \left[ \begin{array}{cc} 0.7 & 0.3 \\ 0.1 & 0.9 \\ 0.2 & 0.8 \\ \end{array} \right] $$
다중 분류 문제이다 보니 Y에서 각 요소를 One hot encoding 방식으로 나타낸 모습을 볼 수 있다.
상위 두 함수를 통해 같은 문제를 해결하는 코드를 나타내면 다음과 같다.
#CrossEntropy.ipynb
import math
y=[0,1,1,0]
hypothesis=[0.3, 0.7, 0.6, 0.2]
sum=0.
for i in range(4):
sum+=-y[i]*math.log(hypothesis[i])-(1-y[i])*math.log(1-hypothesis[i])
crossEntropy=sum/4
print (crossEntropy)
y1Hot=[[1,0],[0,1],[0,1],[1,0]]
#hypothesis1Hot: [prob Y=0, prob Y=1]
hypothesis1Hot=[[0.7,0.3],[0.3,0.7],[0.4,0.6],[0.8,0.2]]
sum1=0.
for i in range(4):
sum2=0.
for j in range(2):
sum2+=-y1Hot[i][j]*math.log(hypothesis1Hot[i][j])
sum1+=sum2
crossEntropy1Hot=sum1/4
print (crossEntropy1Hot)여기서 중요한 점은 결국 Binomial Cross Entropy Function과 Multinomial Cross Entropy Function은 같은 식이라는 점이다.
Neural Network
$$ y=f(\sum{w_ix_i + b}) $$
신경망 모형의 아이디어는 위 식의 결과가 y값이 되도록하는 미지수 w를 구하는 모델이다.
$$ Y = S(w_1x_1 + w_2x_2 + w_3x_3 + b) \\ = \frac{1}{(1 + exp(-(w_1x_1 + w_2x_2 + w_3x_3 + b)))} $$
주목할 점은 활성화 함수로 Sigmoid 함수를 사용할 경우, 위와 같이 신경망 모형이 Logistic Regression 모형이 된다고 한다.
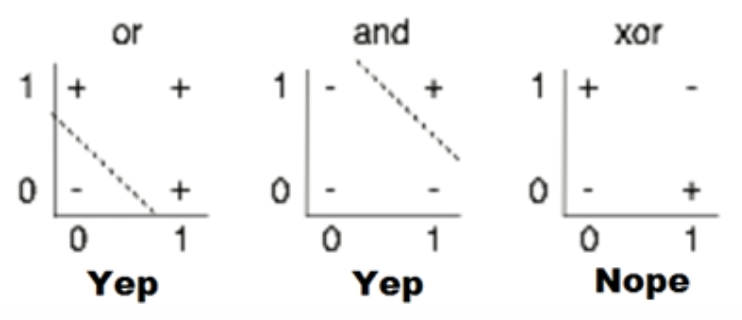
초기 신경망에 대한 역사도 언급해주셨다. 초기에는 왼쪽 두 개의 그래프처럼 Linear한 모형이었기 때문에 OR, AND 문제는 풀 수 있었으나 XOR 문제는 해결할 수 없었다고 한다.

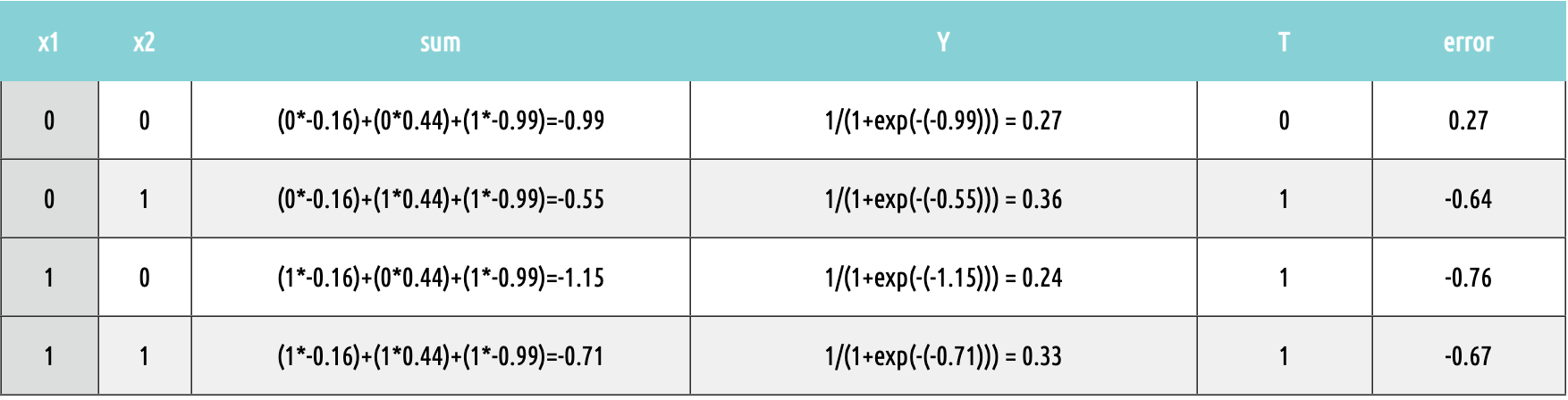
이어서 Neural Network의 전반적인 구동 과정을 살펴보았다. 위 그림은 임의의 W 값으로 연산을 수행하는 과정을 나타낸 것이다. 이를 이용해 아래와 같은 연산을 하고 error가 줄어드는 방향으로 W를 갱신한다.
Sigmoid Function의 성질
$$ Y = S(w_1x_1 + w_2x_2 + b) > 0.5 $$
$$ 즉, (w_1x_1 + w_2x_2 + b) > 0 $$
참고로, Sigmoid Function의 결과가 0.5를 초과한다는 이야기는, 입력된 식의 결과가 0을 초과한다는 이야기와 같다.
가중치 구하기
지금까지는 적절한 가중치가 있을 때 결과를 예측하는 모델을 이야기했다면, 이제는 이때 필요한 적절한 가중치를 역으로 구하는 과정에 대해 이야기해보겠다.
$$ w_i = w_i + (LearningRate)(t -f(net)) $$
위 식은 학습률을 이용해 적절한 가중치를 구하는 과정이다. 이때 $(t-f(net))$은 오차를 구하는 과정이다. 이렇게 구한 오차가 양수면 $f(net)$이 커져야 오차가 줄어들기 때문에 가중치에 일정량을 더한다. 반대로, 오차가 음수면 가중치에 일정량을 뺀다.
신경망 모형 설계하기
1. XOR 문제는 입력이 2개고 출력이 1개다.
2. 히든 레이어는 1개, 노드는 3개로 가정한다.
3. $w_1$은 총 6개의 선으로 2by3 행렬이고, $w_2$는 3개의 선으로 3by1 행렬이다.
4. $b_1$은 1by3 행렬이고 b2는 1by1 행렬이다.
5. $H=xw_1 + b_1$이고 $output=Hw_2+b_2$로 계산한다.
위 조건을 만족하는 신경망 모형을 그리면 다음과 같다.
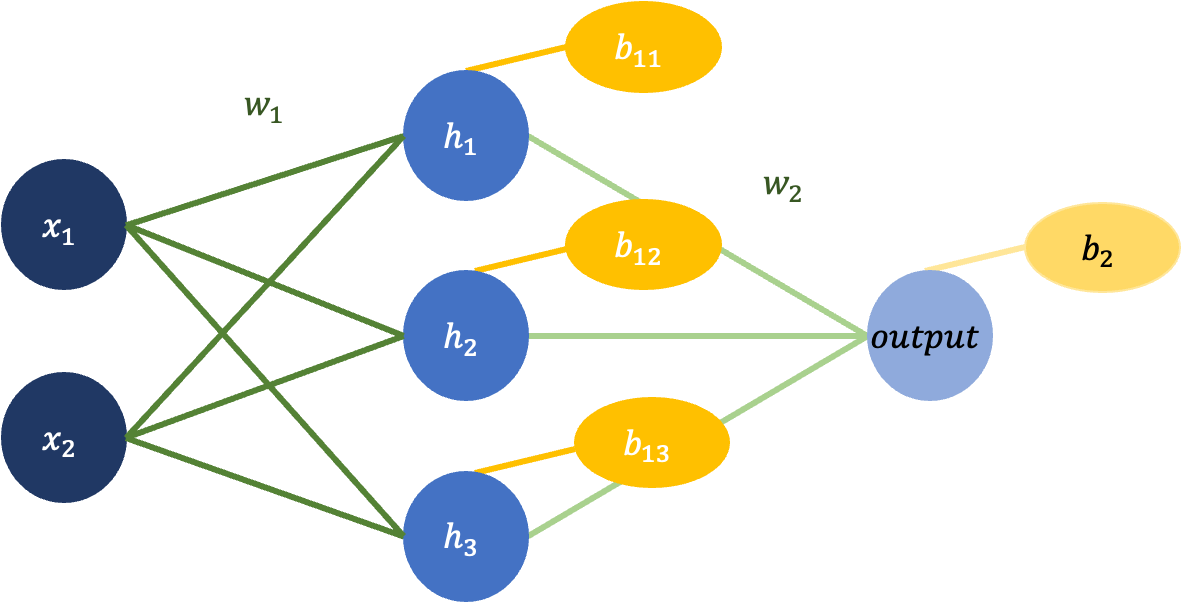
이를 코드로 구현하면 다음과 같다.
# xor.ipynb
import math
import numpy as np
def Sigmoid(x):
return 1/(1+np.exp(-x))
x=np.array([[0,0], [0,1], [1,0], [1,1]])
w1=np.array([[-2, 5, 4], [ 3, 6, 3]])
b1=np.array([2, -2, -5])
w2=np.array([[-4], [ 8], [-8]])
h=Sigmoid(np.dot(x,w1)+b1)
y=Sigmoid(np.dot(h,w2))
print (y)위 코드에서 주목할 점은 Hidden Layer를 추가함으로 XOR 문제를 해결했다는 점이다.
Backpropagation

Backpropagation은 다층 인공 신경망 구조에서 사용하는 학습 알고리즘이다. 일반적으로 Forward 방향으로 계산할 때 어떤 W를 주더라로 Loss에 대한 계산은 가능하다. 이를 반대로 생각해서 Loss의 값이 작아지도록 w, b를 역방향으로 조정하는 아이디어를 구현한 것이 Backpropagation이다.
Backpropagation 과정을 자세히 살펴보면 다음과 같다.
$$ h = S(xw_1),\quad y=S(hw_2),\quad t=Target,\quad S=sigmoid, $$
$$ L=(y-t)^2/2\quad 라고 할 때,$$
$$ \frac{\partial L}{\partial w_2} = h^T\delta _y,\quad \frac {\partial L}{\partial w_1}=x^Th(1-h)w_2 ^T\delta_y $$
위 식에서 $\delta_y$가 재활용되는 모습을 살펴볼 수 있다.
이처럼 $\delta_y$가 재활용되는 성질을 이용하여 출력층으로부터 입력층으로 역으로 가중값을 보정 전파할 수 있음을 보이는 과정이 Backpropagation이다. 이를 이용하면 여러 개의 Hidden Layer가 있어도 역전파 알고리즘을 통해 가중값을 구할 수 있다.
Hidden Node 3개를 갖는 Backpropagation 알고리즘을 코드로 구현하면 다음과 같다.
# xor1.ipynb
import numpy as np
def Sigmoid(x):
return 1/(1+np.exp(-x))
lamda = 1
x=np.array([[1,0,0],[1,0,1],[1,1,0],[1,1,1]])
t=np.array([[0],[1],[1],[0]])
w1=2*np.random.rand(3,3)-1
w2=2*np.random.rand(3,1)-1
for i in range(0,1000):
h=Sigmoid(np.dot(x,w1))
y=Sigmoid(np.dot(h,w2))
deltaY= np.multiply(y-t,np.multiply(y,(1-y)))
temp = np.multiply(w2.transpose(),np.multiply(h,(1-h)))
deltaH = deltaY * temp
w2=w2-np.dot(h.transpose(),lamda*deltaY)
w1=w1-np.dot(x.transpose(),lamda*deltaH)
print(y)
