시계열 분석

시계열 분석(Time Series Forecasting)은 시간에 대해 순차적으로 관측되는 데이터의 집합인 '시계열 데이터'를 분석하는 작업이다. 위 그림은 연도 별 기후 변화를 나타내는 데이터이다. 이 데이터 역시 시계열 데이터에 속한다. 그럼 이러한 시계열 데이터를 왜 분석할까?
시계열 분석의 필요성을 우리가 배울 내용과 연관되게 설명하자면, 현재 상황이 미래 상황에 영향을 미치는 경우에 시계열 분석이 필요하다. 연도 별 기후의 변화 역시 과거의 기후가 현재의 기후에 영향을 미쳐왔고, 미래 기후에도 영향을 미치는 것을 확인할 수 있다.
$$Y_t = \phi Y_{t-1} + \epsilon_t$$
위 수식은 시계열 분석을 할 수 있는 모델을 가장 간단하게 표현한 AR(1)모형이다. AR은 Auto Regressive로, 자기 자신과 이전 시점의 관측치에 의존하는 모형을 의미한다. "1"은 자기 자신과 직전 시점의 관측치만 의존한다는 의미로, 만일 이 숫자가 3이라면 자기 자신과 직전, 그 이전, 또 그 이전까지의 관측치도 의존한다는 의미이다.
$$Y_t = \phi Y_{t-1}+\theta\epsilon_{t-1}+\epsilon_t$$
위 수식은 시계열 분석을 위한 또다른 모형인 ARMA(1, 1)이다. 직전 시점의 오차($\theta \epsilon_{t-1}$)를 아는 것이 현재의 값을 아는 데에 도움이 된다는 아이디어를 반영한 모델이다. 이 모델은 AR모형에서 불규칙적인 현상이라 규정한 부분 중에서도 경향성이 있는 불규칙 현상과 경향성이 없는 불규칙 현상을 구분한 것이 특징이다. 이때 ARMA(p, q)의 파라미터를 각각 p, q로 할 때, 과거 p개 시점의 관측치와 q개 시점의 오차를 활용하겠다는 의미이다.
RNN(Recurrent Neural Network)

RNN은 기존의 신경망 모형을 확장하여 시계열 분석이 가능하도록 만든 모형이다. 위 그림은 순환형 신경망인 RNN을 표현한 것이다. 이전 시점의 결과와 현재 시점의 입력이, 현재 시점의 결과에 영향을 미치는 구조이다.
$$h_t = f(h_{t-1}, x_t)$$
이를 수식으로 나타내면 위와 같다. 이전 시점의 결과($h_{t-1}$)와 현재 시점의 입력($x_t$)이 현재 시점의 결과($h_t$)를 만든다. 이때 활성화 함수로는 $tanh$나 $ReLU$를 주로 사용한다고 한다. 여기서 $h$는 최종 결과는 아니고, 최종 결과를 도출하는 데에 필요한 중간 결과로 보면 된다. (엄밀히는 은닉 상태를 의미한다.)

$$h_t = tanh(W_{hh}h_{t-1} + W_{xh}x_t)$$
위 그림과 수식은 활성화 함수로 $tanh$를 사용한 경우를 나타내고 있다. 현재 시점의 중간 결과($h_t$)를 구하기 위해서 $h_{t-1}$과 $x_t$에 각각의 가중값을 적용한 후, 활성화 함수인 $tanh$를 거치고 있다.
$$y_t = W_{hy}h_t$$
최종적으로 현재 시점의 결과($y_t$)를 도출하는 식이다. 이 과정을 반복해서 과거의 입력이 현재의 입력에 영향을 미치도록 설계한 모형을 RNN이라고 한다.

이러한 RNN은 설계하는 방식에 따라 사진과 같이 one to one ~ many to many 모델을 구현할 수 있다. 각 모델에 대한 예시를 간략히 언급하면 다음과 같다.
- one to one: 다음으로 작성될 문자나 단어를 예측하는 모형
- one to many: 이미지 하나를 입력하고 많은 이미지를 제작하는 모형
- many to one: 주어진 문장에 대해 긍정, 부정을 판별하는 모형
- many to many: 문장을 번역하는 모형
Char RNN
Char RNN은 문자 단위로 예측하는 RNN 모형이다. 문자 단위로 예측할 때 RNN을 사용하는 이유는 무엇일까?
RNN은 이전에 언급했듯이 과거의 입력이 현재의 결과에 영향을 주는 경우에 사용한다. 우리가 사용하는 언어에서도 과거에 특정 문자가 입력되었을 때 다음으로 입력될 문자에는 경향성이 있으므로, 충분히 예측이 가능하다. 이 경우 역시 RNN을 이용하여 처리가 가능하기 때문에 RNN을 사용한다.

문자를 학습시키기 위해서는 위와 같이 수치벡터화 하는 One hot encoding 작업을 거친다.
참고로, One hot encoding을 하기 때문에 한글을 학습함에 있어서도 큰 문제가 없다고 한다.

위 그림은 입력된 값에 따라 다음으로 따라올 값을 잘 맞출 수 있도록 가중값을 조절하는 과정을 나타낸다. output layer로 표시된 파란색 박스 내 초록색으로 표시된 인덱스의 값이 가장 크게 되도록 Backpropagation을 통해 가중값을 조정해나간다.
import numpy as np
from tensorflow.keras import layers
# One hot encoding for each char in 'hello'
h = [1, 0, 0, 0]
e = [0, 1, 0, 0]
l = [0, 0, 1, 0]
o = [0, 0, 0, 1]
# One cell RNN input_dim (4) -> output_dim (3). sequence: 5
x_data = np.array([[h, e, l, l, o]], dtype=np.float32)
print(x_data, x_data.shape)
hidden_size = 3
rnn = layers.SimpleRNN(units=hidden_size, return_sequences=True, return_state=True)
outputs, states = rnn(x_data)
print(outputs, outputs.shape)
print(states, states.shape)위 코드는 앞서 그림으로 설명한 문자 학습 코드이다.
이때, outputs는 히든 레이어의 모든 시퀀스에 대한 값을 기억하고 있고 states는 마지막 시퀀드의 히든 레이어 값만 가지고 있다.
굳이 이렇게 분류한 이유는, 마지막 시퀀스의 히든 레이어가 이전까지의 학습 내용을 내포하고 있기 때문에 이 값만 알고 있는 것도 의미가 있을 때가 있기 떄문이다.
# hidden node 크기는 마음대로 정할 수 있다.
n_hidden = 5
model = Sequential()
model.add(layers.SimpleRNN(n_hidden, input_shape=(None, input_size), return_sequences=True))
model.add(layers.TimeDistributed(layers.Dense(output_size, activation='softmax')))위 코드는 'hell'를 입력했을 때 'ello'가 출력되도록 Many to many 모형을 학습시키는 과정이다.
이때, 'TimeDistributed' 를 사용해서 Many to one 방식을 Many to many 방식으로 구현하였다.
Word Embedding
앞서 문자 학습 과정에서는 문자 별로 One hot encoding 과정을 거쳤다. 그러나, 이를 문장 단위를 실행하려고 하면 그 작업이 너무 복잡해진다. 이때 학습 과정에서의 복잡도를 줄이고자 입력 데이터의 차원을 축소하는 Embedding을 수행한다.
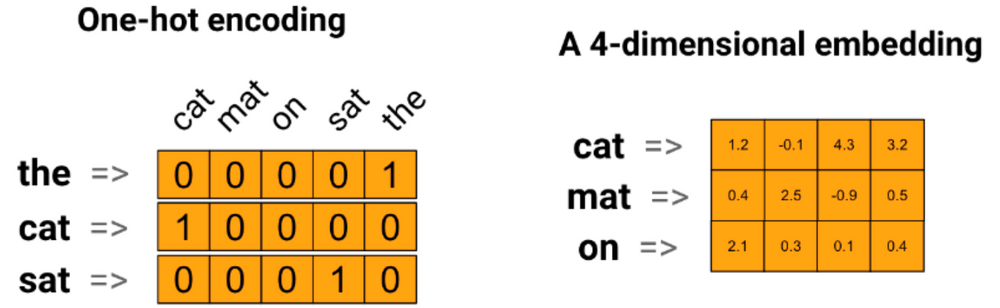
위 그림은 One hot encoding 데이터를 Embedding Vector로 변환한 예시이다. 그림에서 볼 수 있듯이 5차원 데이터를 4차원 데이터로 축소시켰다.
Embedding Vector로 변환하면 데이터의 차원을 축소한다는 이점을 얻을 수 있을 뿐 아니라, 단어의 유사도를 표현할 수도 있다는 장점이있다. 예를 들어 'love'와 'like'를 이전과 같이 One hot encoding 과정을 거쳐 학습시킨다면 이 두 단어는 완전히 다른 개념으로 인식할 것이다. 그러나, Embdding 과정을 거치면 이 두 단어가 비슷한 상황에서 쓰이는 유의어임을 나타낼 수 있는 장점이 있다.
CBOW
CBOW(Continuous Bag Of Words)는 Embedding Vector를 구하는 방법 중 하나로, 주변 단어들로부터 중심 간어를 예측하는 신경망 모형이다.

위 그림은 CBOW의 원리를 보이고 있다. 중심 단어를 옮겨가며 주변 단어와의 관계에 대한 데이터셋을 만들고, 학습해나간다.
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])
history = model.fit(x_data, y_data, epochs=30)위 코드는 CBOW 과정 중 일부만 나타낸 것이다. 'sparse_categorical_crossentropy' 구문을 통해 입력 데이터와 출력 데이터에 One hot encoding 과정을 거치지 않아도 알아서 값을 구해주도록 했다.
LSTM
앞서 배운 RNN은 과거 정보를 이용하여 현재 정보를 예측하는 모형이다. 때문에 정상적인 구동을 위해서는 과거 정보를 모두 알아야 하는데, 이때 시퀀스의 길이가 너무 길어져 Gradient Vanishing 문제가 발생할 수 있다.
⬇️ Gradient Vanishing 설명
Gradient vanishing 문제는 신경망 학습에서 역전파 과정에서 기울기(gradient) 값이 점차적으로 소멸되어 가중치 업데이트가 제대로 이루어지지 않는 현상을 말한다. 이는 깊은 신경망에서 특히 발생할 수 있는 문제로, 네트워크의 깊이가 깊어질수록 심화될 수 있다.
이러한 문제를 해결하기 위해 과거 정보에 중요도를 부여해 판별 및 구분하는 LSTM(Long Short Term Memory)이 탄생했다.
$$h_t = f(h_{t-1}, x_t) \rightarrow C_t = f_t \cdot C_{t-1} + i_t \cdot h_t$$
LSTM을 수식으로 표현하면 위와 같다.

위 그림은 LSTM을 시각화한 것이다. '과거 상태를 얼마나 잊을 것인가'를 결정하는 Forget Gate와 '현재 입력을 얼마나 중요하게 여길 것인가'를 결정하는 Input Gate를 통해 과거 정보와 현재 정보의 중요도를 결정한다.

그러나, LSTM 역시 문장이 너무 길어지면 Gradient Vanishing 문제가 발생한다. 이를 극복하기 위해 양방향으로 설계된 BiLSTM이 탄생했다.
BiLSTM의 왼쪽은 Many to many 모형이고, 오른쪽은 Many to one 모형이다. 그림에서 볼 수 있듯이 LSTM 두 개가 동시에 순방향과 역방향으로 출력을 예측한다. 그 결과 일반적인 LSTM보다 나은 결과를 얻을 수 있다고 한다.
Stacked RNN
매우 긴 문장을 학습하기 위해서는 Batch와 Stacked RNN을 적용하기도 한다.
Batch는 이전에 배웠듯이, 입력 데이터의 크기를 나누고 부분 별로 학습을 진행하는 방식으로, 학습의 속도는 개선할 수 있지만 모형의 정확도가 떨어진다는 문제가 발생한다. 이러한 문제를 방지하기 위해서는 Cell의 수를 증가시켜야 한다.
이를 위해 Recurrent Layer를 여러 개로 확장하는 Stacked RNN을 사용한다.
'대학교 공부 > 데이터마이닝 (2023)' 카테고리의 다른 글
| 12주차 - Auto Encoder, PCA, Noise Reduction, Anomaly Detection, Colorization, Image Search (0) | 2023.06.18 |
|---|---|
| 11주차 - Batch Normalization, Kernal Regularization, Transfer Learning (0) | 2023.06.18 |
| 10주차 - Convolutional Layer, Fashion Mnist Data, Cifar10 Data (0) | 2023.06.18 |
| 8주차 - CNN 실습, 파라미터 수 계산 (0) | 2023.06.18 |
| 7주차 - CNN, Convolution Layer, Zero Padding (0) | 2023.05.23 |