공간정보를 다룰 때, 두 지점 사이의 거리를 계산하는 일은 굉장히 흔하다. 그런데 이 거리 계산이 단순하지 않을 수도 있다. 특히 좌표계가 위도와 경도로 표현되어 있을 때는, 지구가 둥글다는 사실을 무시할 수 없게 된다. 이때 등장하는 개념이 바로 True Geodetic 거리이다.
평면 거리와 뭐가 다를까?

우리가 흔히 사용하는 거리 계산은 평면 위의 직선 거리다. 예를 들어 네이버 지도에서 어떤 카페까지 몇 미터인지 나오는 그 거리. 이건 대부분 유클리디안 거리(Euclidean Distance)라고 해서, x, y 좌표 간의 직선 거리를 의미한다.
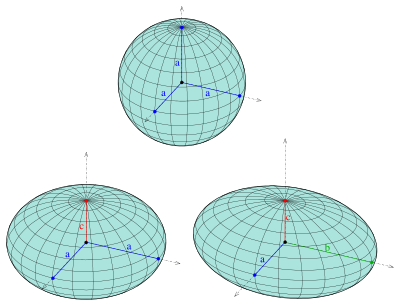
하지만 지구는 평면이 아니다. 지구는 둥글고, 정확히 말하면 타원체(Ellipsoid) 형태를 하고 있다. 그래서 위도(latitude)와 경도(longitude)로 표현된 두 지점 사이의 실제 거리를 계산할 땐, 지구의 곡률을 고려해야 한다. 이게 바로 True Geodetic 거리의 핵심이다.
왜 중요할까?
짧은 거리에서는 평면 거리나 True Geodetic 거리나 큰 차이가 나지 않는다. 하지만 거리가 수 km, 수백 km로 커질수록 오차는 눈에 띄게 커진다.
예를 들어 서울과 부산 사이의 거리를 평면으로 계산하면 약간 짧게 나올 수 있다. 반면, True Geodetic 거리를 사용하면 지구 표면 위에서 가장 짧은 경로(=측지선, geodesic line)를 기준으로 계산하므로 실제에 더 가깝다.
이런 정확성이 중요한 경우는 아래와 같다:
- 항공 경로 계산
- 국가 간 거리 측정
- 재난 피해 범위 분석
- 정확한 반경 기반 검색 (예: 반경 5km 내 병원 찾기)
실제 데이터베이스에서는 어떻게 처리할까?
공간 데이터베이스나 GIS 도구에서는 True Geodetic 계산을 지원하는 경우가 있다. 다만 별도 함수나 설정이 필요할 수도 있다.
예를 들어,
- PostGIS에서는 ST_DistanceSphere, ST_DistanceSpheroid 같은 함수로 타원체 기반 계산이 가능하다.
- Oracle Spatial에서도 SDO_GEOM.SDO_DISTANCE 함수에서 단위를 km로 지정하면 타원체 기반 거리를 계산한다.
- QGIS 같은 도구에서는 기본적으로 투영 좌표계가 설정되어 있을 수 있으니, 지리 좌표계(WGS 84 등)를 사용하거나 설정을 조정해야 한다.
정리하며
True Geodetic 거리는 평면적인 계산에 비해 연산 비용이 크지만, 정확한 결과를 원할 때는 반드시 고려해야 할 방식이다. 특히 지리 좌표계 기반의 데이터를 다룬다면, 평면 거리만으로는 안심할 수 없다.
정확한 공간 분석을 원한다면, 거리 계산이 True Geodetic인지 꼭 확인해보자.
'개인 학습 > 공간정보' 카테고리의 다른 글
| Geocoder - 주소 정보로 좌표 얻기(파이썬 코드 포함) (0) | 2024.05.17 |
|---|---|
| QGIS - 동일 레이어 내 속성별 개수 세기(Counting with Database) (0) | 2024.05.17 |
| QGIS - 동일 레이어 내 정보들을 다른 색으로 나타내기 (0) | 2024.05.17 |
| QGIS - CSV 파일 지도에 나타내기 (2) | 2024.05.17 |