10주차 - SQL(비절차적 언어), DDL DML 심화, 관계대수(셀렉션, 프로젝션, 집합, 파티션 곱, 조인, 디비전)

SQL의 역할

1. 릴레이션 정의
2. 무결성 제약조건 명세
3. 정보 갱신
4. 정보 검색

 SQL은 대부분의 RDBMS의 표준 질의어이기 때문에 알아야 한다. 이러한 SQL 문의 역할은 위와 같으며, 이들 중 가장 자주 쓰이는 기능이 '검색'이다.

 

SQL의 개요

 SQL은 비절차적 언어, 즉 선언적 언어이다. 때문에 사용자는 자신이 원하는 바에 해당하는 'What'에 대한 정보만 입력하고, 정보를 제공 받기 위한 과정에 해당하는 'How'에 대한 과정에 대해서는 명시하지 않는다.

 

그리고 이 SQL문을 RDBMS가 해석하여 'How'에 해당하는 과정을 스스로 정의하여 결과를 가져온다.

 

이러한 SQL은 '데이터 정의어', '데이터 조작어', '데이터 제어어'로 구성된다.

 

데이터 정의어(DDL: Data Definition Language)

 데이터 정의어는 데이터베이스의 뼈대를 구축하기 위한 과정을 수행하는 언어이다. 이에 대한 역할을 구문 별로 살펴보자.

 

//스키마의 생성과 제거

CREATE SCHEMA MY_DB AUTHORIZATION kim; //1
DROP SCHEMA MY_DB RESTRICT; //2
DROP SCHEMA MY_DB CASCADE; //3

DDL의 첫 번째 역할은 바로 '스키마의 생성과 제거'이다. 참고로 스키마는 릴레이션, 도메인, 제약조건, 뷰, 권한 등을 그룹화하기 위해 사용하는 개념이다.

 

1번 구문은 이러한 스키마를 생성하는 명령어이다. 'MY_DB'라는 스키마를 생성하면서 'kim'에게 권한을 부여하고 있다.

 

2번 구문은 스키마를 제거하는 명령어이다. 'RESTRICT' 구문을 추가함으로 삭제하는 과정에서 데이터가 존재하는 부분이 있다면, 해당 스키마에 대한 삭제 명령을 거부할 수 있도록 명시하였다.

 

3번 구문 역시 스키마를 제거하는 명령어이다. 'CASCADE' 구문을 추가함으로 삭제하는 과정에서 데이터가 존재하는 분이 있다면, 관련 내용들을 일일이 방문하여 모두 제거하도록 명시하였다.

 

//릴레이션 정의

CREATE TABLE EMPLOYEE
(EMPNO      INTEGER NOT NULL,
 EMPNAME    CHAR(10),
 TITLE      CHAR(10),
 MANAGER    INTEGER,
 SALARY     INTEGER,
 DBO        INTEGER,
 PRIMARY KEY(EMPNO),
 FOREIGN KEY(MANAGER) REFERENCES EMPLOYEE(EMPNO),
 FOREIGN KEY(DNO) REFERENCES DEPARTMENT(DEPTNO));

DDL의 두 번째 역할은 '릴레이션 정의'이다. 위 구문에서는 괄호와 콤마, 세미 콜론의 위치, 주 키 및 외래 키를 명시하는 방법에 대해 익혀두는 것이 중요하다.

 

• VARCHAR(n): 최대 n 바이트까지의 '가변 길이' 문자열
• BLOB: Binary Large OBject로, 2MB 내외의 이미지, 사운드와 같은 비문자형 데이터를 저장할 수 있는 데이터 타입

애트리뷰트를 선언할 때 데이터 타입 및 도메인을 설정하는 모습을 볼 수 있다. 위 데이터 타입들은 데이터베이스에서 선언될 수 있는 데이터 타입 중 특별한 데이터 타입을 소개한 것이다.

 

//도메인 생성

CREATE DOMAIN DEPTNAME CHAR(10) DEFAULT '개발';

DDL의 세 번째 역할은 '도메인 생성'이다. 위 구문에서는 'DEPTNAME'이라는 이름의 도메인을 생성하고 있다.

 

도메인은 스키마나 애트리뷰트와는 다른 개념이다. 도메인을 생성한다 함은 앞서 스키마 생성 시 데이터 타입 및 도메인을 정하기 위해 'CHAR'이나 'INT'를 명시한 것처럼 사용되는 새로운 기준을 만드는 과정이라고 볼 수 있다.

 

//릴레이션 제거
DROP TABLE DEPARTMENT;

//릴레이션 수정
ALTER TABLE EMPLOYEE ADD PHONE CHAR(13);

//인덱스 생성
CREATE INDEX EMPDNO_IDX ON EMPLOYEE(DNO);

이외에도 DDL은 위와 같은 구문들을 통해 다양한 역할(릴레이션 제거, 릴레이션 수정, 인덱스 생성, ..)을 수행할 수 있다.

 

CREATE TABLE EMPLOYEE
(...
 FOREIGN KEY(DNO) REFERENCES DEPARTMENT(DEPTNO)
         ON DELETE SET DEFAULT ON UPDATE CASCADE
);

DDL을 통해 제약조건을 설정할 때에는 위와 같이 'ON' 구문을 통해 수행하는 작업에 따라 제약조건을 다르게 적용할 수도 있다.

 

ALTER TABLE STUDENT ADD CONSTRAINT STUDENT_PK
      PRIMARY KEY(STNO);

ALTER TABLE STUDENT DROP CONSTRAINT STUDENT_PK

DDL을 통해 위와 같이 제약조건을 추가 및 삭제할 수도 있다.

 

데이터 조작어(DML: Data Manipulation Language)

SQL의 두 번째 구성요소인 DML은 데이터를 갱신하는 역할을 한다.

 

//투플 삽입

INSERT
INTO RELATION_NAME(ATTRIBUTE1, ATTRIBUTE2, ..)
VALUES (VALUE1, VALUE2, ..);

DML의 첫 번째 역할은 '릴레이션에 투플을 삽입'하는 것이다. 위와 같은 구문이 입력되었다면 사실상 RDBMS 내부에서는 다음과 같은 과정이 이루어진다.

 

1. 메타 데이터를 통해 해당 릴레이션이 존재하는지 확인
2. 메타 데이터를 통해 해당 애트리뷰트가 존재하는지 확인
3. 입력되는 값이 도메인 제약조건을 만족하는지 확인
4. 그외 제약조건(키, 참조)을 위배하지 않는지 확인

참고로 이러한 맥락에서, 참조하는 자식 릴레이션에 투플을 삽입할 때는 참조 무결성 제약조건에 위배될 수 있다.

 

//투플 삭제

DELETE 
FROM RELATION_NAME
WHERE CUSTOM_CONDITION;

DML의 두 번째 역할은 '투플을 삭제'하는 것이다. 참고로 위 구문에서 'WHERE' 절에 대한 내용을 따로 지정하지 않으면 해당 릴레이션의 모든 레코드를 삭제한다.

 

이러한 DELETE문을 수행할 때는 INSERT 문과는 반대로, 참조되는 부모 릴레이션에서 삭제 연산을 수행할 때 참조 무결성 제약조건에 위배될 수 있다.

 

//애트리뷰트 값 수정

UPDATE RELATION_NAME
SET ATTRIBUTE1 = VALUE1, ATTRIBUTE2 = VALUE2, ..
WHERE ATTRIBUTE = COSTUM_CONDITION

DML의 세 번째 역할은 '애트리뷰트 값을 수정'하는 것이다. 

 

이러한 UPDATE문을 수행할 때는 기본 키나 외래 키에 해당하는 애트리뷰트 값이 수정될 때, 참조 무결성 제약조건에 위배될 수 있다.

 

---

관계 대수(Relation Algebra)란?

 관계 대수란, '어떻게 질의를 수행할 것인가', 즉 'How'를 기술하는 절차적 언어이다. 주로 SQL을 구현하고 최적화하기 위한 DBMS의 내부적 언어로 사용된다.

 

비록 SQL은 비절차적 언어이지만, SQL 내부에서 사용되는 언어가 어떤 의미이며 어떠한 과정을 통해 처리되는지를 알 필요가 있기 때문에 우리는 절차적 언어인 관계 대수를 배운다.

 

관계 대수의 특징

 관계 대수는 기본적인 연산자들의 집합으로 이루어졌다. 또한 객체지향 언어처럼 기존의 릴레이션들로부터 새로운 릴레이션을 생성할 수 있다고 한다.

 

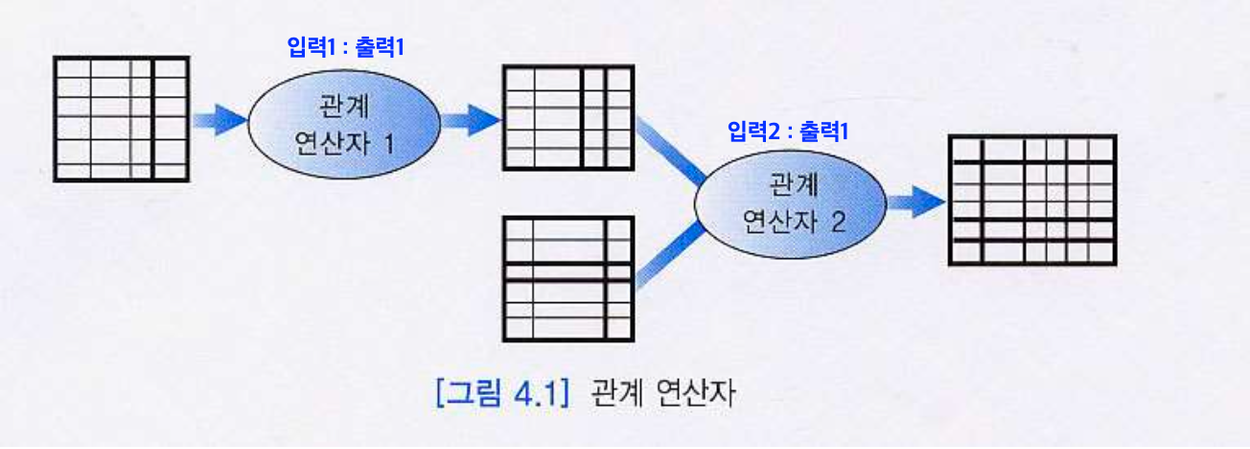
또한 관계 대수는 단일, 혹은 두 개의 릴레이션을 입력 받아 하나의 결과 릴레이션을 생성한다는 특징이 있다. 그리고 이러한 결과 릴레이션은 당연하게도 다른 관계 연산자의 입력 릴레이션으로 사용될 수 있다. (이러한 과정을 점차 복잡하고 길게 늘여 놓다 보면 웬만한 관계 대수 식을 직접 제작할 수 있다.)

 

관계 대수 속 새로운 릴레이션

관계 대수에서는 새로운 릴레이션이 소개된다. 실렉션, 프로젝션, 카티션 곱, 디비전과 같은 생소한 개념도 소개되고 있다. 

 

1, 1	1, 2	..	1, n
2, 1	2, 2	..	2, n
..	..	..	..
m, 1	m, 2	..	m, n

앞으로 릴레이션 관계를 설명하기 위해 위와 같은 개념을 소개 및 도입하려 한다.

 

릴레이션 R이 위 표와 같이 존재한다고 가정하자. 그렇다면 애트리뷰트 수에 해당하는 차수(Degree)는 n이고, 투플의 수에 해당하는 카디날리티 수는 m이다.

 

특정 연산을 수행한 결과 릴레이션은 Res로 표현한다고 하자. 차수는 deg(R)로 표현하고, 카디날리티 수는 |R|로 표현할 것이다.

 

실렉션 연산자

실렉션 연산자를 통해서는 한 릴레이션으로부터 조건을 만족하는 투플들의 부분 집합을 생성한다. 

 

$$Res = \sigma_P(R)$$

연산자는 위와 같이 표시한다. 이러한 결과 릴레이션의 특징은 다음과 같다.

1. $P$는 실렉션 조건으로, Predicate라고 불림
2. $deg(Res) = n$: 애트리뷰트의 형식은 변하지 않음
3. $0 <= |Res| <= m$: 결과 릴레이션은 기존 릴레이션의 카디날리티 수를 넘지 못함

 

프로젝션 연산자

프로젝션 연산자를 통해서는 '애트리뷰트 리스트'에 명시된 애트리뷰트들만 가져온다. 표로 살펴보면 열 단위로 추출한다.

 

$$Res = \pi_{AL}(R)$$

연산자로는 위와 같이 표시한다. 이러한 결과 릴레이션의 특징은 다음과 같다.

1. $AL$은 Attribute List임
2. $deg(Res) = |AL| <= n$: 결과 릴레이션의 차수는 애트리뷰트 리스트의 크기와 같으며, 이는 다시 기존 릴레이션의 차수를 넘지 못함
3. $|Res| = m$: 레코드의 형식은 변하지 않음

 

합집합 호환(Union Compatible)

집합 연산자는 관계 대수에서 나오는 새로운 릴레이션은 아니다. 그래도 살펴보면 합집합, 교집합, 차집합 연산자가 있다.

 

이러한 집합 연산을 수행하기 위해서는 두 릴레이션이 '합집합 호환(Union Compatible)'을 만족해야 한다는 조건이 존재한다.

 

연산을 수행하고자 하는 릴레이션이 각각 R과 S라고 할 때, 합집합 호환 조건을 살펴보면 다음과 같다.

1. $deg(R) = deg(S)$
2. $max(|R|, |S|) <= |Res| <= |R| + |S|$
3. 모든 경우에 $domain(R) = domain(S)$

 

합집합 연산자

두 릴레이션에 하나라도 존재하는 투플들의 집합을 나타낸 릴레이션이다. 결과 릴레이션에서 중복된 투플들은 반드시 제외한다는 특징이 있다. 또한 결과 릴레이션의 차수는 R 혹은 S의 차수와 같고, 애트리뷰트 이름들도 R 혹은 S 애트리뷰트의 이름과 같다는 특징이 있다.

 

이러한 합집합 연산을 활용한 실전 예제를 살펴보면 다음 과 같다.

 

김창섭이 속한 부서 혹은 개발 부서의 부서번호를 검색하라

 

 

 

교집합 연산자

두 릴레이션에서 모두 존재하는 투플들의 집합을 나타낸 릴레이션이다. 결과 릴레이션에서 나타나는 특징은 다음과 같다.

1. $0<=|Res|<= min(|R|, |S|)$

 

차집합 연산자

두 릴레이션 R과 S가 있다고 할 때, R에는 속하지만 S에는 속하지 않는 투플들로 이루어진 집합을 결과로 나타낸다. 결과 릴레이션에서 나타나는 특징은 다음과 같다.

1. $0<=|Res|<=|R|$
2. R과 S 사이의 교환법칙이 적용되지 않음: 연산 순서 바뀌면 완전히 다른 결과가 나옴

 

카티션 곱 연산자

 

두 릴레이션의 투플들로 이룰 수 있는 '모든 조합'을 결과 릴레이션으로 나타내는 연산자이다. 그러다보니 결과 릴레이션의 크기가 너무 커질 수 있기에 현업에서 유용하게 사용하는 연산자는 아니라고 한다.

 

조인 연산자

두 릴레이션에서 연관된 투플들을 결합하는 연산자이다. 현업에서도 꽤나 유용하게 쓰인다고 한다. 이러한 조인 연산자에는 세타조인, 동등조인, 자연조인, 외부조인, 세미조인 등이 있다.

 

세타조인과 동등조인 연산자

이 두 연산자의 개념은 비슷하다. 왜냐하면 여기서 말하는 세타($\theta$)에 부등호와 같은 연산자를 넣으면 곧 동등조인이 되기 때문이다.

 

이러한 연산자들의 특징은 다음과 같다.

1. 조인할 때 사용된 애트리뷰트는 양 릴레이션에 중복되게 존재해야 함
2. 비교하는 애트리뷰트끼리의 도메인이 같아야 함
3. 동등조인은 카티션곱 결과에 조건에 맞게 실렉션하는 것과 같음

 

자연조인 연산자

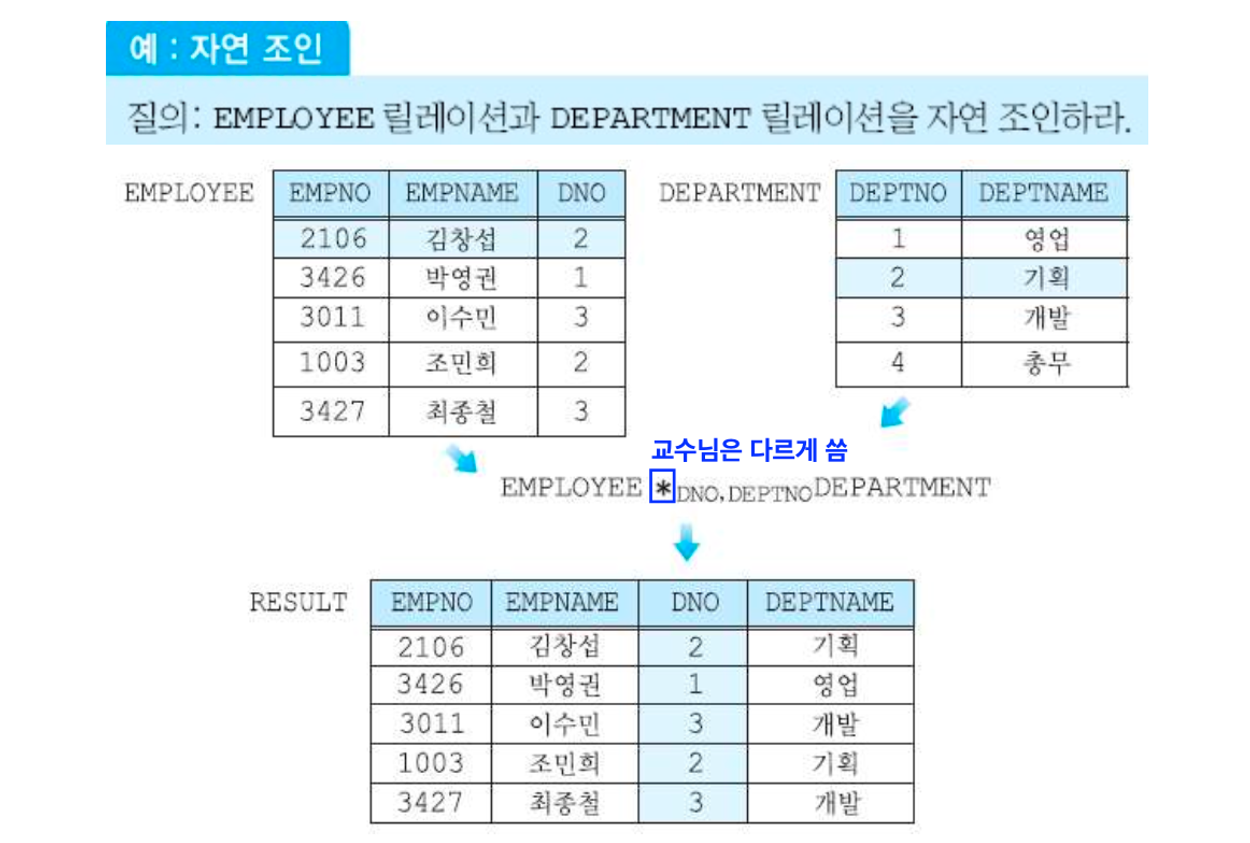
자연조인은 세타조인의 특징 중 하나인 "사용된 애트리뷰트는 양 릴레이션에 중복되게 존재해야 함"에서 발전한 특징을 가지고 있다. 바로 하나의 애트리뷰트만 결과 릴레이션에 남기도록 하는 연산자이다. 조인 연산자들 중 가장 자주 사용되는 연산자라고 한다.

 

디비전 연산자

1. 릴레이션 R에 A1, A2, .., An, B1, B2, .., Bm이 존재한다고 하자
2. 릴레이션 S에 B1, B2, .., Bm만 존재한다고 하자
3. R과 S를 디비전한 결과 릴레이션에는 A1, A2, .., An만 남는다.

디비전 연산자를 개념적으로 설명하면 위와 같다. 

 

더 간단하게 그림으로 설명하면 위와 같다. $R ÷ S$라고 할 때, $R$ 중에서 $S$에 있는 값이 존재하는 레코드의 나머지 값들을 반환하는 모습을 볼 수 있다.